DSA Sheet by Technical Mickey

Morris Inorder Traversal of a Binary tree

Problem Description

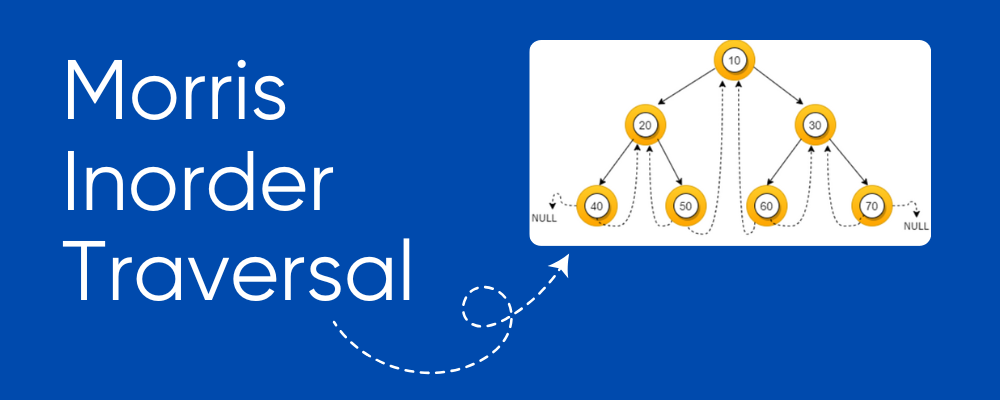
Given a binary tree, perform an inorder traversal (Left → Root → Right) without using recursion or extra stack space. The goal is to achieve O(1) space complexity by modifying the tree structure temporarily.

Intuition

In a standard inorder traversal, we use recursion (which requires implicit stack space) or an explicit stack to keep track of nodes.

Morris Inorder Traversal eliminates the need for extra memory by creating temporary links (threading) between nodes. These links help us traverse the tree without revisiting nodes unnecessarily.

The key idea is:

If a node has no left child, print the node and move to its right.
If a node has a left child, find its inorder predecessor (rightmost node in the left subtree).
- If the predecessor’s right child is NULL, create a temporary thread pointing to the current node.
- If the predecessor’s right child points to the current node, remove the thread, print the node, and move to the right subtree.

Solution Approach

Initialize current as the root.
Loop until current is NULL:
- Case 1: If current.left is NULL → Print current, move to current.right.
- Case 2: If current.left exists → Find the inorder predecessor (rightmost node in current.left).
  - If predecessor.right == NULL:
    - Create a temporary link (predecessor.right = current).
    - Move current to its left child.
  - Else:
    - Remove the temporary link (predecessor.right = NULL).
    - Print current and move to current.right.

Solution Implementation (Java)

				
					public class MorrisInorderTraversal {
    public static void morrisTraversal(TreeNode root) {
        TreeNode current = root;
        while (current != null) {
            if (current.left == null) {
                System.out.print(current.val + " ");
                current = current.right;
            } else {
                // Find inorder predecessor
                TreeNode predecessor = current.left;
                while (predecessor.right != null && predecessor.right != current) {
                    predecessor = predecessor.right;
                }

                // Create a temporary thread
                if (predecessor.right == null) {
                    predecessor.right = current;
                    current = current.left;
                }
                // Remove the thread and process the node
                else {
                    predecessor.right = null;
                    System.out.print(current.val + " ");
                    current = current.right;
                }
            }
        }
    }

Time and Space Complexity Analysis

Time Complexity: O(N)

Each node is visited at most twice (once when traversed and once when the thread is removed).
The inner while loop runs at most O(H) times in total, where H is the height of the tree.
For a balanced tree, H = log N, so the overall complexity remains O(N).

Space Complexity: O(1)

Unlike recursive or stack-based methods, no extra space is used except for a few temporary pointers.
The modifications to the tree are temporary, so no additional data structures are required.

Example Execution

Binary Tree Structure

Inorder Output using Morris Traversal

Advantages of Morris Traversal

✅ O(1) Space Complexity (No recursion or extra stack)
✅ Efficient for Large Trees (Saves memory)
✅ Preserves Inorder Sequence

Disadvantages

❌ Modifies Tree Temporarily (Requires careful restoration)
❌ Extra Pointer Manipulations (Can be tricky to implement)

Conclusion

Morris Inorder Traversal is a powerful technique for space-efficient binary tree traversal. It is especially useful when recursion or extra memory usage is not allowed, making it a valuable tool for technical interviews and competitive programming. 🚀

Technical Mickey