Given a binary array nums, return the maximum number of consecutive 1‘s in the array if you can flip at most one 0.
Example 1:
Input: nums = [1,0,1,1,0]
Output: 4
Explanation:
- If we flip the first zero, nums becomes [1,1,1,1,0] and we have 4 consecutive ones.
- If we flip the second zero, nums becomes [1,0,1,1,1] and we have 3 consecutive ones.
The max number of consecutive ones is 4.
Example 2:
Input: nums = [1,0,1,1,0,1]
Output: 4
Explanation:
- If we flip the first zero, nums becomes [1,1,1,1,0,1] and we have 4 consecutive ones.
- If we flip the second zero, nums becomes [1,0,1,1,1,1] and we have 4 consecutive ones.
The max number of consecutive ones is 4.
Constraints:
1 <= nums.length <= 105nums[i]is either0or1.
Problem Intuition
The goal is to find the longest stretch of consecutive 1s in a binary array, but with one twist: you are allowed to flip at most one 0 into a 1.
How the Two-Pointer Approach Works
Think of it as a Sliding Window:
- We use two pointers, left (l) and right (r), to represent the current “window” of the array we’re analyzing.
- This window will always contain at most one
0flipped to a1.
Track Zeros in the Window:
- We keep a counter
k, which starts at1(because we can flip one0). - Each time we encounter a
0in our window, we “spend” this flip by decrementingk.
When the Window Becomes Invalid:
- If
kbecomes negative, it means we’ve encountered more than one0in the window. At this point, the window is invalid. - To fix this, we shrink the window by moving the left pointer (
l) to the right, until the window contains at most one0(i.e.,kis no longer negative).
Keep Expanding the Window:
- As the right pointer (
r) moves forward, and the window continues to expand. If it becomes invalid, we adjust the left pointer (l) as described above.
Track the Largest Window:
- At every step, the size of the window (
r - l) represents the number of consecutive1s (with at most one0flipped). By the end of the iteration, this will naturally give us the longest sequence.
Key Idea
We don’t explicitly store a “maximum length” variable. Instead:
- The size of the window grows as we expand
r. - It only shrinks temporarily when
kbecomes negative, and then it resumes expanding once the window is valid again. - This ensures the longest window is automatically tracked.
Explanation with Example
Imagine the array: [1, 0, 1, 1, 0, 1, 1, 1]
- Start with
l = 0, r = 0, k = 1. - As
rmoves:- At
r = 1, you encounter a0. Decrementkto0. - At
r = 4, you encounter another0. Decrementkto-1. Now the window is invalid. - Move
lto the right until the window becomes valid again (k = 0).
- At
By the end of the loop, the largest window size (r - l) will give you the result.
Final Code Here:
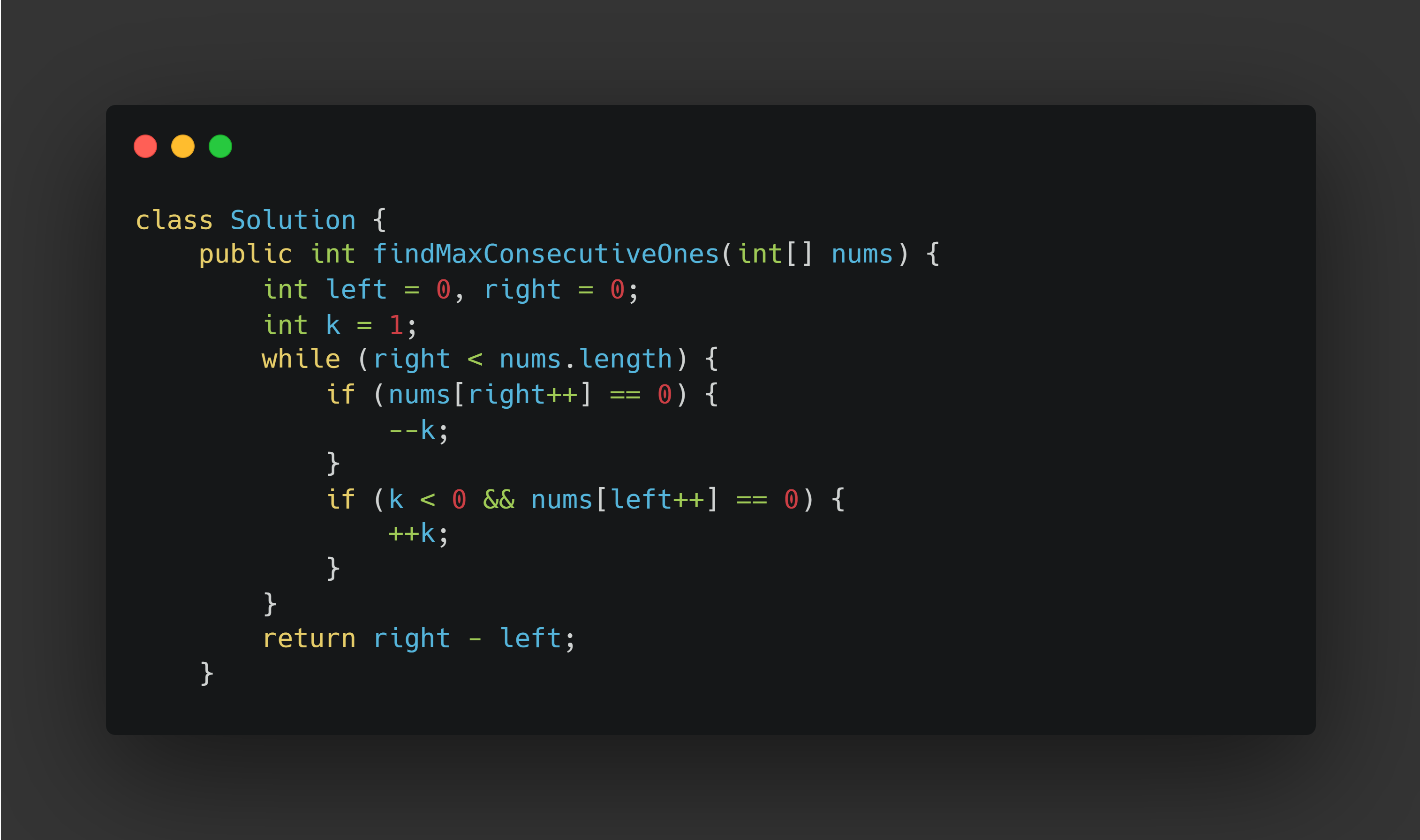
Time and Space Complexity
The time complexity of the given code is O(n), where n is the length of the input list nums. This efficiency is achieved because the code uses a two-pointer technique that iterates through the list only once. The pointers l (left) and r (right) move through the array without making any nested loops, thus each element is considered only once during the iteration.
The space complexity of the code is O(1), which means it uses constant additional space regardless of input size. No extra data structures that grow with the input size are used; the variables left, right, and k take up a constant amount of space.

