DSA Sheet by Technical Mickey

Set Matrix Zeroes

Problem Description

You are given a matrix A of size N x M where each row is sorted in ascending order. Your task is to find and return the overall median of the matrix.

Constraints

1 <= N, M <= 10^5
1 <= N * M <= 10^6
1 <= A[i] <= 10^9
N * M is always odd, ensuring a single median value exists.

Notes

No extra memory is allowed.
Rows are numbered from top to bottom, and columns are numbered from left to right.

Intuition

To solve this problem efficiently:

Binary Search on Value Range: The matrix has sorted rows, which allows us to perform a binary search on the possible range of values, i.e., from the smallest to the largest element in the matrix.
Counting Smaller Elements: For a given value, count how many elements in the matrix are smaller than or equal to it. This can be efficiently computed using binary search on each row.
Median Definition: The median is the middle element when all elements are sorted. For an odd-sized matrix, it is located at position .

Solution Approach

The solution employs the following steps:

1. Find the Value Range

Identify the smallest and largest values in the matrix.
- The smallest value is the first element of the first row.
- The largest value is the last element of the last row.

2. Binary Search for the Median

Use binary search between the smallest and largest values to determine the median.
For each mid-point in the binary search, count how many elements in the matrix are less than or equal to that mid-point.
Adjust the binary search range based on whether the count is less than or greater than the desired position.

3. Count Elements Efficiently

Use a helper function to count how many elements in a sorted row are smaller than or equal to a given value. This is done using binary search on the row.

Implementation

Here is the Java implementation of the solution:

				
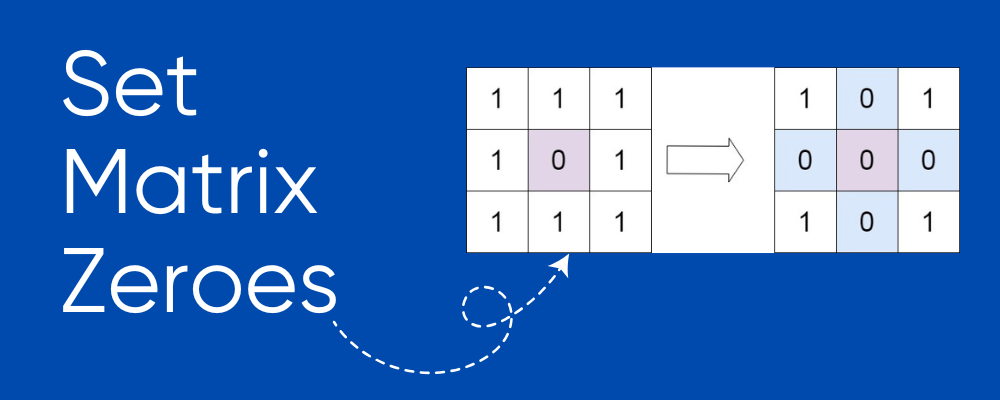
					class Solution {
    public void setZeroes(int[][] matrix) {

        int N = matrix.length;
        int M = matrix[0].length;
        int col0 = 1; // Variable to track if the first column needs to be zeroed

        // Step 1: Use the first row and column as markers
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0; // Mark the row
                    if (j != 0) {
                        matrix[0][j] = 0; // Mark the column
                    } else {
                        col0 = 0; // Mark the first column
                    }
                }
            }
        }

        // Step 2: Update the matrix based on markers
        for (int i = 1; i < N; i++) {
            for (int j = 1; j < M; j++) {
                if (matrix[0][j] == 0 || matrix[i][0] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }

        // Step 3: Update the first row if needed
        if (matrix[0][0] == 0) {
            for (int j = 0; j < M; j++) {
                matrix[0][j] = 0;
            }
        }

        // Step 4: Update the first column if needed
        if (col0 == 0) {
            for (int i = 0; i < N; i++) {
                matrix[i][0] = 0;
            }
        }
    }
}

Complexity Analysis

Time Complexity: O(N * M)
- Single pass through the matrix for marking and another for updating.
Space Complexity: O(1)
- No extra space used apart from input matrix.

Technical Mickey